Math 21a Fall 2019
Multivariable Calculus

Bouncing at a corner
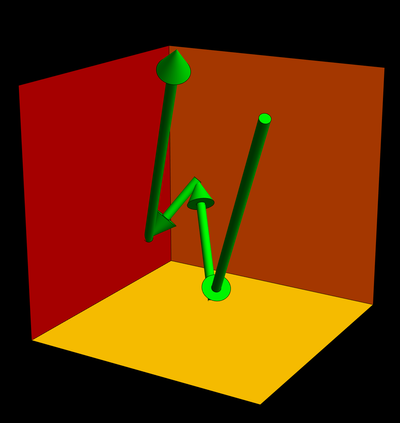
| You have seen in HW 5, that if a light ray bounces into a corner, it comes out parallel in a different direction. This is a theme in an office season (see the movie to the right). A java script animation of a ball reflection can be seen here . |
Direct Media Links: Webm, Ogg Ipod |
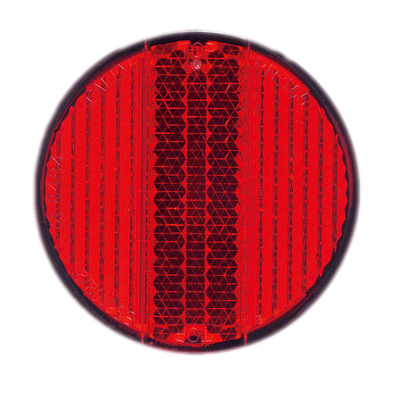
| Reflectors you have on the bike have lots of little corners inside. Incoming light will reflect back to the place where it comes from. Click on the picture to the left to see it larger. |
|
T[{{x_,y_},{u_,v_}}]:=Module[{r=0.03},
{{a,b},{c,d}}={{x,y}+{u,v},{u,v}};
If[y>1-r,{{a,b},{c,d}}={{a,2-2r-b},{c,-d}}];
If[y<r,{{a,b},{c,d}}={{a,2r-b},{c,-d}}];
If[x<r,{{a,b},{c,d}}={{2r-a,b},{-c,d}}];
If[x>1-r,{{a,b},{c,d}}={{2-2r-a,b},{-c,d}}];
{{a,b},{c,d}}]
DynamicModule[{p={}},
EventHandler[Graphics[{Hue[Random[]],PointSize[0.1],
Point[Dynamic[p=Map[T,p];Map[First,p]]]},
PlotRange->{{0,1},{0,1}},Background->Yellow],
"MouseDown":>(AppendTo[p,{MousePosition["Graphics"],
{Random[]/90,-Random[]/90}}])]]
|

|